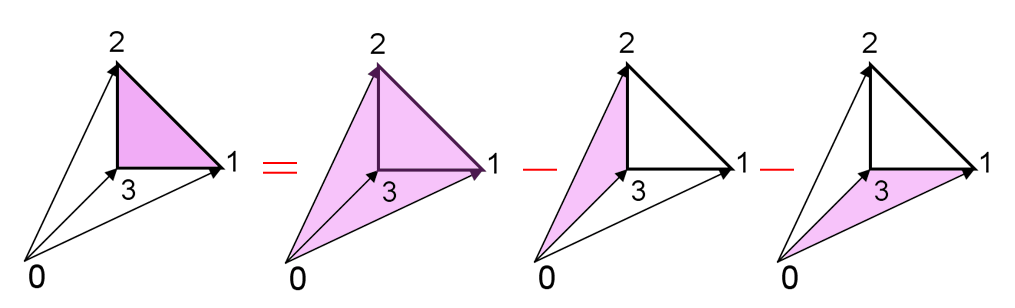
倍横距法を用いて多角形の面積を求める ベクトルの外積 倍横距法では、ベクトルの外積（ベクトル積）を利用します。 xy平面上のベクトル ａ1 ＝（x1 , y1 , 0）と ａ2 ＝ （x2 , y2 , 0）とすると、 ａ1 と ａ2 の外積は、 ａ1Xａ2 ＝ (0 , 0 , x1*y2−x2*y1) また、 ａ1 と ａ2 を二辺とする平行四辺形の面積は、 ｜ａ1｜・｜ａ2｜sinθ ＝ ｜ａ1Xａ2｜ ＝ ｜x1*y2−x2*y1｜ 三角形の面積 xy平面上の三角形１２３の面積を、ベクトルの外積を利用して求める。 下図のように三角形と点０を置く。 図より、三角形１２３の面積は、三角形０１２の面積から三角形０２３の面積と三角形０３１の面積を引けばよい。 例題として、各点の座標を ０：（０，０，０）、１：（４，２，０）、２：（２，４，０）　３：（２，２，０） とすると 各三角形の面積は、平行四辺形の面積の半分であるから、ベクトルの外積を用いて 三角形０１２　 (x1*y2−x2*y1)/２ ＝ (４*４−２*２)/２ ＝ ６ 三角形０２３　 (x2*y3−x3*y2)/２ ＝ (２*２−２*４)/２ ＝ −２ 三角形０３１　 (x3*y1−x1*y3)/２ ＝ (２*２−４*２)/２ ＝ −２ 三角形１２３　 ６−２−２ ＝ ２ ここで、外積の成分が符号付きで求まり、各面積の加減がなされる。 一方、三角形１２３は、底辺：２　高さ：２であるから 三角形の面積は、底辺*高さ/２より、２*２/２ ＝ ２　となり、ベクトルの外積を利用した結果と一致する。 多角形の面積 xy平面上のＮ角形の面積を、ベクトルの外積を利用して求める。 i番目の点の座標を（xi , yi , 0）とすると、Ｎ角形の面積Ｓは、 Ｓ ＝ ｜ｓ1＋ｓ2＋・・・＋ｓＮ−１＋ｓＮ｜/２ ここで、ｓi ＝ xi*yi+1-xi+1*yi ただし、ｓＮ ＝ xＮ*y1-x1*yＮ 倍横距法を用いて、市区町村の行政区画の面積を求める